フラクタル図形

前置き

人工知能について調べていたらなぜかいつの間にかフラクタルに流れ着いていた。
かなりきれいなものが多かったので自分でもフラクタル図形を描画してみようと思い、Processingでプログラムをいくつか生成した。

コッホ雪片

ArrayList<Koch>koch=new ArrayList<Koch>();
ArrayList<Koch>kochSTK=new ArrayList<Koch>();

void setup() {
  size(800, 800);
  strokeWeight(0);
  stroke(#ffffff);
  fill(255);
  noFill();
  int n=6;
  for (int i=0; i<n; i++) {
    float d=i*TWO_PI/n;
    float r=width*0.37;
    koch.add(new Koch(width/2+cos(d)*r, height/2+sin(d)*r, 
      width/2+cos(d+TWO_PI/n)*r, height/2+sin(d+TWO_PI/n)*r));
  }
  noLoop();
}

void mousePressed() {
    redraw();
}

void draw() {
  background(0);

  beginShape();
  for (Koch k : koch) {
    k.update();
    kochSTK.addAll(k.mkKoch());
  }
  endShape();
  koch.clear();
  koch.addAll(kochSTK);
  kochSTK.clear();

  println("step : "+frameCount);
}

public class Koch {
  float sx, sy, ex, ey;
  public Koch(float sx, float sy, float ex, float ey) {
    this.sx=sx;
    this.sy=sy;
    this.ex=ex;
    this.ey=ey;
  }

  public void update() {
    vertex(sx, sy);
    vertex(ex, ey);
  }

  public ArrayList<Koch>mkKoch() {
    ArrayList<Koch>koch=new ArrayList<Koch>();
    float l=sqrt((sq(sx-ex)+sq(sy-ey)))/3;
    float a=atan2(ey-sy, ex-sx)+PI/3;
    float x=lerp(sx, ex, 1./3.);
    float y=lerp(sy, ey, 1./3.);
    float xx=x+cos(a)*l;
    float yy=y+sin(a)*l;
    koch.add(new Koch(sx, sy, x, y));
    koch.add(new Koch(x, y, xx, yy));
    x=lerp(sx, ex, 2./3.);
    y=lerp(sy, ey, 2./3.);
    koch.add(new Koch(xx, yy, x, y));
    koch.add(new Koch(x, y, ex, ey));
    return koch;
  }
}

レヴィドラゴン

ArrayList<Koch>koch=new ArrayList<Koch>();
ArrayList<Koch>kochSTK=new ArrayList<Koch>();

void setup() {
  size(800, 800);
  strokeWeight(1);
  stroke(255);
  fill(255);
  noFill();
  koch.add(new Koch(width*3/4, height/4, width*3/4, height*3/4));
  noLoop();
}

void mousePressed() {
    redraw();
}

void draw() {
  background(0);

  beginShape();
  for (Koch k : koch) {
    k.update();
    kochSTK.addAll(k.mkKoch());
  }
  endShape();
  koch.clear();
  koch.addAll(kochSTK);
  kochSTK.clear();
}

public class Koch {
  float sx, sy, ex, ey;

  public Koch(float sx, float sy, float ex, float ey) {
    this.sx=sx;
    this.sy=sy;
    this.ex=ex;
    this.ey=ey;
  }

  public void update() {
    vertex(sx, sy);
    vertex(ex, ey);
  }

  public ArrayList<Koch>mkKoch() {
    ArrayList<Koch>koch=new ArrayList<Koch>();
    float l=sqrt((sq(sx-ex)+sq(sy-ey))/2);
    float a=atan2(ey-sy, ex-sx);
    float xx=sx+cos(a+QUARTER_PI)*l;
    float yy=sy+sin(a+QUARTER_PI)*l;
    koch.add(new Koch(sx, sy, xx, yy));
    koch.add(new Koch(xx, yy, ex, ey));
    return koch;
  }
}

ヘイウェイドラゴン

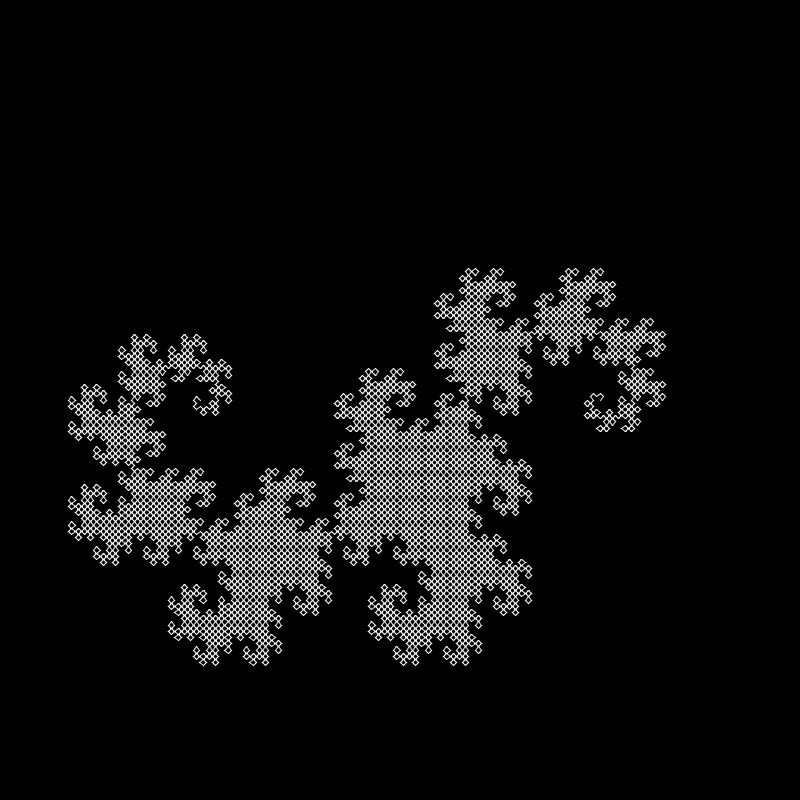
ArrayList<Koch>koch=new ArrayList<Koch>();
ArrayList<Koch>kochSTK=new ArrayList<Koch>();

void setup() {
  size(800, 800);
  strokeWeight(1);
  stroke(255);
  fill(255);
  noFill();
  koch.add(new Koch(width/4, height/2, width*3/4, height/2));
  noLoop();
}

void mousePressed() {
    redraw();
}

void draw() {
  background(0);

  beginShape();
  int i=0;
  for (Koch k : koch) {
    k.update();
    kochSTK.addAll(k.mkKoch((++i)%2*2-1));
  }
  endShape();
  koch.clear();
  koch.addAll(kochSTK);
  kochSTK.clear();
}

public class Koch {
  float sx, sy, ex, ey;

  public Koch(float sx, float sy, float ex, float ey) {
    this.sx=sx;
    this.sy=sy;
    this.ex=ex;
    this.ey=ey;
  }

  public void update() {
    vertex(sx, sy);
    vertex(ex, ey);
  }

  public ArrayList<Koch>mkKoch(int i) {
    ArrayList<Koch>koch=new ArrayList<Koch>();
    float l=sqrt((sq(sx-ex)+sq(sy-ey))/2);
    float a=atan2(ey-sy, ex-sx);
    float xx=sx+cos(a+QUARTER_PI*i)*l;
    float yy=sy+sin(a+QUARTER_PI*i)*l;
    koch.add(new Koch(sx, sy, xx, yy));
    koch.add(new Koch(xx, yy, ex, ey));
    return koch;
  }
}
<||

*** シェルピンスキーギャスケット
[f:id:turane_gaku:20150301001212p:plain]
>|processing|
Sierpinski s;

void setup() {
  size(800, 800);
  noStroke();
  fill(255);
  float r=width*0.4;
  float d=-HALF_PI;
  s=new Sierpinski(new PVector(width/2+cos(d)*r, height/2+sin(d)*r), 
                   new PVector(width/2+cos(d-=TWO_PI/3)*r, height/2+sin(d)*r), 
                   new PVector(width/2+cos(d-=TWO_PI/3)*r, height/2+sin(d)*r));
  noLoop();
}

void mousePressed() {
    redraw();
}

void draw() {
  background(0);

  s.update();
}

public class Sierpinski {
  private PVector p[];
  private Sierpinski s[];

  public Sierpinski(PVector...p) {
    this.p=p;
  }

  public void update() {
    if (s==null) {
      triangle(p[0].x, p[0].y, p[1].x, p[1].y, p[2].x, p[2].y);
      mkSierpinski();
    } else {
      for (int i=0; i<s.length; i++)
        s[i].update();
    }
  }

  private void mkSierpinski() {
    s=new Sierpinski[3];
    PVector l=new PVector((p[0].x+p[1].x)/2, (p[0].y+p[1].y)/2);
    PVector r=new PVector((p[0].x+p[2].x)/2, (p[0].y+p[2].y)/2);
    PVector d=new PVector((p[1].x+p[2].x)/2, (p[1].y+p[2].y)/2);
    s[0]=new Sierpinski(p[0], l, r);
    s[1]=new Sierpinski(l, p[1], d);
    s[2]=new Sierpinski(r, d, p[2]);
  }
}

コッホ雪片の値をいじくりまわしていたら、なかなかきれいな図形ができた。

ギャスケットを応用してカーペットを作った。

カーペットの値をちょこちょこ変更してカントールの塵を作った。

感想

単純な法則でここまで複雑な図形を描けるのは中々に面白いし。興味深い。
L-systemというものも見つけたので次回はそれについて考える。

L-system - つらねの日記