つらねの日記

プログラムの進捗やゲームをプレイした感想などを書き連ねる日記。

マンデルブロ集合の生成に成功した

はじめに

マンデルブロ集合とは

Mandelbrot set - Wikipedia, the free encyclopedia

マンデルブロ集合は以下の漸化式z_nが無限大に発散しない複素数cの集合である．

{ \displaystyle z_0 = 0 }

{ \displaystyle z_{n+1} = z_n ^ 2 + c }

cの実数部分をx軸，虚数部分をy軸に取ったものがよくみられるフラクタル図形である．

人は日々進化しているんだ

昨日，「マルデンブロ集合」という単語を見かけ，「マンデルブロ」だろと思いながらも 一応確認を行うため，調べたところ，恒例の図形が表われた．

その図形を眺めていると，昔フラクタルについて 勉強した際 に見かけたものの， 全く理解することができなかったことを思いだした． その理由として以下の7点を挙げることができる．

  • 他のフラクタル図形と同じノリで，必要な部分だけ計算する感じだと勘違いしていた．
  • そもそもcの存在を理解しておらず，z_nがマンデルブロ集合だと勘違いしていた．
  • 複素数をJavaで扱うのが面倒だな，，と思った．
  • 実数だけで扱えるというサンプルがWikipediaにあったが，x,yという文言から，勝手に座標系と勘違いしていた．
  • xn,ynをポインティングしてみて違うじゃんと叫んでいた．
  • 発散だの収束だのどう判断するのか理解できなかった．
  • 記事をしっかりと読んでいなかった．

今回，https://en.wikipedia.org/wiki/Mandelbrot_setや http://azisava.sakura.ne.jp/mandelbrot/を眺め， 無事理解し，processingにて図形を生成することが出来たので，忘れぬように書き記しておく． processingでは他の言語におけるcomplexなどといった便利なクラスは存在しないので， 実数部と虚数部を分けて，それぞれ自分で計算する必要がある．

f:id:turane_gaku:20160206014856p:plain

図形生成のアルゴリズム

他のフラクタル図形との違い

フラクタル図形で理解が容易く，生成が簡単なものとして，シェルピンスキーのギャスケットが挙げられる．

https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%AB:SierpinskiTriangle.PNG

これは三角形の中に4つの三角形があるという理解が容易い，フラクタル図形である． 作る際も普通に再帰や，成分を細かく成長させてゆくだけで事足りる．

対して，マンデルブロ集合は単純に再帰で書くだけ，といったものではなく， ある数学的性質を満す虚数の集合を数直線上にプロットしてみたらフラクタル図形になっている といったもので単純にはいかない． つまり，連続的に次，次と求められるものではなく，虚数を大量に集め，分別するというステップを踏む必要がある． 可能な限り，連続な状態になるように分割した虚数全てを，マンデルブロ集合に属すか，属さないかを判断し， それを描画するというステップを取る必要があるようだ．

収束と発散の判断

ある虚数cがマンデルブロ集合に属すか否かの判断には以下の漸化式が発散するかどうか，を用いる．

{ \displaystyle z_0 = 0 }

{ \displaystyle z_{n+1} = z_n ^ 2 + c }

つまりそれぞれの虚数に対して，いちいち面倒な計算を行う必要がある．

この漸化式が収束するか発散するかどうかの判断は http://azisava.sakura.ne.jp/mandelbrot/ に詳しい説明があるが， {|z_n| > 2}を用いれば良いらしい．

複素数を実数部と虚数部に分割する

Javaにはcomplexなどといった便利なクラスはデフォルトでは入っていないので， 実数部と虚数部に式を分割する必要がある． ここで，

{ \displaystyle c = A + Bi }

{ \displaystyle z = a + bi }

とする．

{ \displaystyle z_{n+1} = z_n ^ 2 + c }

{ \displaystyle a_{n+1} = a_n ^ 2 - b_n ^ 2 + A }

{ \displaystyle b_{n+1} = 2 * a_n * b_ni + B }

と式変形できる．

複素数の絶対値に関しては， 複素数{z=a+bi}とあらわしたとき，

{ \displaystyle |z|^2 = a ^ 2 + b ^ 2 }

となるため，発散するか否かの判断には[tex:a2 + b2 > 4]を用いる．

マンデルブロ集合か否か

まとめると，ある虚数A+Biが与えられたとき，その数がマンデルブロ集合か否かを判断するためには 以下の関数を用いる．

boolean ismandelbrot(double A, double B){
  double a = 0;
  double b = 0;
  for(int i = 0; i < 500; i++) {
    double aa = a * a - b * b + A;
    double bb = 2 * a * b + B;
    a = aa;
    b = bb;
    if (a * a  + b * b >= 4) return false;
  }
  return true;
}

現在は500項目まで求めているが，場合によってはより深い部分まで求める必要がでてくるだろう．

まとめ

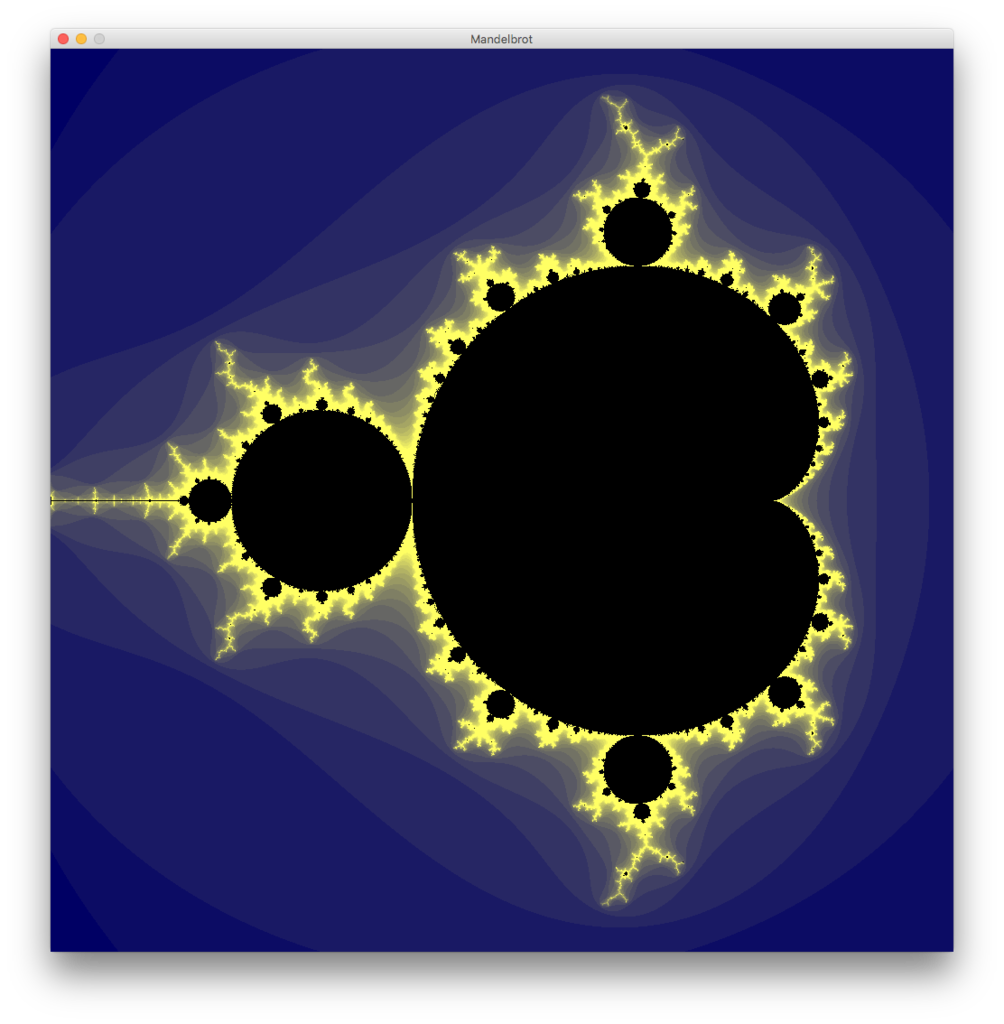
A，Bをそれぞれx軸y軸にプロットし，適当な感じで色付けするプログラムが以下の通りになる．

Mandelbrot.pde

double scale = 400;
int div = 20;

void setup() {
  size(1000, 1000);
  noLoop();
}

int ismandelbrot(double A, double B){
  double a = 0;
  double b = 0;
  for(int i = 0; i < 500; i++) {
    double aa = a * a - b * b + A;
    double bb = 2 * a * b + B;
    a = aa;
    b = bb;
    if (a * a  + b * b >= 4) return i;
  }
  return -1;
}

void draw() {
  for(int b = 0; b < height; b++) {
    for(int a = 0; a < width; a++) {
      int m = ismandelbrot((a - width * 7 / 10) / scale, (b - height / 2) / scale);
      if(m == -1)
        set(a, b, color(0));
      else if (m % 3 == 0)
        set(a, b, color(100, m * 255 / div, m * 255 / div));
      else if (m % 3 == 1)
        set(a, b, color(m * 255 / div, m * 255 / div, 100));
      else
        set(a, b, color(m * 255 / div, 100, m * 255 / div));
    }
  }
}

今回は無事マンデルブロ集合を描画することができた． 昔は理解が出来なかったこと，実装が不可能だった事柄も， 時を経て知識を身に付けることで理解できることが増えていくのだろう．

昔作成した物事を再び作りなおしてみたり，見返してみることも大切なのではないか と気付くことができた．